What is Bandwidth?

Introduction to Bandwidth
According to Meriam-Webster Dictionary, the definition of bandwidth is
1: a range within a band of wavelengths, frequencies, or energies; especially : a range of radio frequencies which is occupied by a modulated carrier wave, which is assigned to a service, or over which a device can operate
2: the capacity for data transfer of an electronic communications system (graphics consume more bandwidth than text does); especially : the maximum data transfer rate of such a system

Anyway, the engineers always do not take the definition from the dictionary as a simple answer. So, what is bandwidth anyway? Engineers always mention about “bandwidth” when dealing with oscilloscope, probe, trace, connectors, etc. Sometimes, due to budget limitation, engineers complain about not enough bandwidth or limited bandwidth. So what is all this fuss about bandwidth?

Ever think about why the sampling oscilloscope with 50GS/s (GS/s: sampling per second) costs so much higher than the digital phosphor oscilloscope with just 1GS/s? The reason is very simple: the scope with 50GS/s has much higher bandwidth than the scope with 1GS/s. The bandwidth of the scope with 1GS/s is about 100MHz whereas the bandwidth of the scope with 50GS/s is 50GHz. May be examples can give you a better idea about bandwidth.

Below is a scope shot of a 50MHz square wave (generated by a FPGA device) captured on a sampling oscilloscope with 50GS/s.

Below is a scope shot of the 50MHz square wave from the similar source as above, captured on a digital phosphor oscilloscope with 1GS/s.


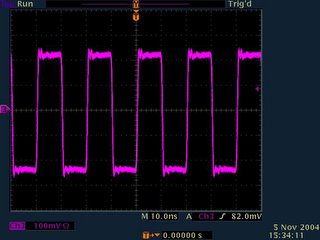
As you can see, it doesn't seem to have much difference from both the captured scope shots of a 50MHz square wave, but sometimes looks can be deceiving. Let's check out the rising time of this 50MHz square wave. Again, both scope shots (zoomed in from the previous shots) are shown here for your reference.
Square wave rising-edge captured on a 50GS/s scope:


Square wave rising-edge captured on a 1GS/s scope:


So, as you can see, the rising-edge of the 50MHz square wave actually is within ps (pico-second)range, but the 1GS/s scope tells you that the rising-edge takes almost 1ns (nano-second). Anyway, this is still acceptable for 50MHz square wave.

Let's now measure 250MHz square wave (also generated by FPGA) on both the 50GS/s scope and 1GS/S scope.
This is measured on the 50GS/s scope:


This is measured on the 1GS/s scope:


Needless to say, the 250MHz square wave looks more like a trapezoidal wave on the 1GS/s scope.

How does 500MHz square wave look like on both scope? Here are the scope shots.
500MHz square wave measured on 50GS/s scope:


500MHz square wave measured on 1GS/s scope and it no longer looks like square wave:


Finally, this is how the 1GHz square wave looks like on the 50GS/s and 1GS/s scope, respectively. As you can see, the 1GHz not only looks more like a sinusoidal wave from the 1GS/s scope, its amplitude is also much smaller.



I believe all the above scope shots can prove to you the importance of bandwidth of a oscilloscope. Not only that, the bandwidth of a probe can also affect the results seen on the oscilloscope. The scope shot below is captured using a 4GHz FET probe and a SMA cable on a 7GHz storage scope. The signal measured is a 3.125Gbps signal generated by a Stratix GX FPGA device.

So, in conclusion, what are the considerations for the bandwidth? There are several rules of thumb when considering the bandwidth of an instrument.
1. Minimum bandwidth should be at least 5 times of the expected measured highest frequency.
2. If you are interested to measure the rise time, the minimum bandwidth should be 0.45/(rise time). Otherwise, the rise time that you have measured is inaccurate. For an example, look at the rise time of the 50MHz square wave captured above from different scopes.
3. Or, the minimum bandwidth is up to the 9th harmonic of the highest frequency, of course, higher the better. If you are not sure of what is 9th harmonic, then you can read my previous posts, History and Beauty of Sine Function and Building Square Wave from Fourier Series. That is the reason I said that the Fourier Series plays an important role in today's world and this is just one of the thousands examples or applications that have a close relationship with Fourier.